고정 헤더 영역
상세 컨텐츠
본문
q4) 금광
- n * m 크기의 금광이 있다 금광은 1 * 1크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있다
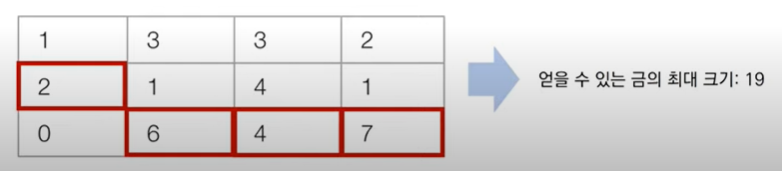
- 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작, 맨 처음에는 첫 번째 열의 어느 행에서든 출발할 수 있다 이후에 m -1번에 걸쳐 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 한다. 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기 출력
조건) 첫째 줄이 테스트 케이스 T가 입력된다 매 테스트케이스 다음줄에 n과 m이 공백으로 구분되어 입력 되어야 한다 그 다음 금의 크기를 공백으로 구분하여 입력
ex)
2 케이스 수
3 4 첫번째 케이스 3 * 4크기
1 3 3 2 2 1 4 1 9 6 4 7
4 4 두번째 케이스 4 * 4 크기
1 3 1 5 2 2 4 1 5 0 2 3 8 6 1 2
- 첫번째 케이스
| 1 | 3 | 3 | 2 |
| 2 | 1 | 4 | 1 |
| 9 | 6 | 4 | 7 |
-> 출력예시 19
- 두번째 케이스
| 1 | 3 | 1 | 5 |
| 2 | 2 | 4 | 1 |
| 5 | 0 | 2 | 3 |
| 8 | 6 | 1 | 2 |
-> 출력예시 16
하나만 하겠다면
1 케이스 수
3 3 케이스 크기 3 * 3
1 3 3 2 1 4 0 6 4
- 금광의 모든 위치에 대하여 다음의 세 가지만 고려하면 된다
1. 왼쪽 위에서 오는 경우
2. 왼쪽 아래서 오는 경우
3. 왼쪽에서 오는 경우
- 세 가지 경우 중에서 가장 많은 금을 가지고 있는 경우를 테이블에 갱신해주어 문제 해결

- array[i][j] = i행 j열에 존재하는 금의 약
- dp[i][j] = i행 j열까지의 최적의 해 (얻을 수 있는 금의 최댓값)
- 점화식은 다음과 같다

- 이때 테이블에 접근할 때마다 리스트의 범위를 벗어나지 않는지 체크
- 편의상 초기 데이터를 담는 변수 array를 사용하지 않아도 된다
- 바로 DP테이블에 초기 데이터를 담아서 다이나믹 프로그래밍을 적용할 수 있다
- 금광 문제를 다이나믹 프로그래밍으로 해결하는 과정

-> 입력값
# 테스트 케이스(Test Case) 입력
for tc in range(int(input())):
# 금광 정보 입력
n, m = map(int, input().split())
array = list(map(int, input().split()))
# 다이나믹 프로그래밍을 위한 2차원 DP 테이블 초기화
dp = []
index = 0
for i in range(n):
dp.append(array[index:index + m])
index += m
# 다이나믹 프로그래밍 진행
for j in range(1, m):
for i in range(n):
# 왼쪽 위에서 오는 경우
if i == 0: left_up = 0
else : left_up = dp[i - 1][j - 1]
# 왼쪽 아래서 오는 경우
if i == n - 1: left_down = 0
else : left_down = dp[i + 1][j -1]
# 왼쪽에서 오는 경우
left = dp[i][j - 1]
dp[i][j] = dp[i][j] + max(left_up, left_down, left)
result = 0
for i in range(n):
result = max(result, dp[i][m - 1])
print(result)
-> 출력값
C:\Users\admin\PycharmProjects\ML_EX\venv\Scripts\python.exe C:/Users/admin/PycharmProjects/ML_EX/study06.py
1
3 3
1 3 3 2 1 4 0 6 4
12
종료 코드 0(으)로 완료된 프로세스
풀이)
# 테스트 케이스(Test Case) 입력
for tc in range(int(input())):
- 처음 입력받는 값 만큼 아래 조건을 반복하기(테스트
# 금광 정보 입력
n, m = map(int, input().split())
array = list(map(int, input().split()))
- n, m값 즉 케이스 크기를 공백을 기준으로 입력 받고 정수형으로 변환해서 리스트로 만들기
- 여기서 이어지는 금과 정보는 공백을 기준으로 한줄에 이어서 입력 받는다
- 3 * 3크기이면
- 위에서 구현한 코드에서 입력의 틀린 예시
1 케이스 수
3 3 케이스 크기 3 * 3
1 3 3
2 1 4
0 6 4 이렇게 입력받는게 아닌
- 위에서 구현한 코드에서 입력의 올바른 예시
1 케이스 수
3 3 케이스 크기 3 * 3
1 3 3 2 1 4 0 6 4
# 다이나믹 프로그래밍을 위한 2차원 DP 테이블 초기화
dp = []
index = 0
- dp테이블을 빈 리스트로 만들고 앞에까지는 리스트의 초기화 방법을 사용했지만 지금은 2차원이기 때문에 index =0 으로 리스트의 값을 0으로 초기화
for i in range(n):
dp.append(array[index:index + m])
index += m
- 0부터 n-1까지 하나씩 꺼내는 값을 i라고하고 아래를 반복
- dp테이블에 열의 크기만큼 슬라이싱해서 빈 dp테이블에 채운다
- 예를들어 n이 3이면 i 는 0 부터 2까지
| DP 테이블 | 인덱스 0 | 인덱스 1 | 인덱스 2 |
| i = 0 | 1 (좌표: 0,0) | 3 (좌표: 0,1) | 3 (좌표: 0,2) |
| i = 1 | 2 (좌표: 1,0) | 1 (좌표: 1,1) | 4 (좌표: 1,2) |
| i = 2 | 0 (좌표: 2,0) | 6 (좌표: 2,1) | 4 (좌표: 2,2) |
# 다이나믹 프로그래밍 진행
for j in range(1, m):
- 1에서부터 열 - 1까지 즉 3을 입력받았으니 2까지 1 ~ 2까지 하나씩 꺼내는 값을 j 로하고 아래 반복
for i in range(n):
- n도 3을 입력 받았으니 0~ 2까지 순서대로 꺼내는 값을 i라고 하고 아래 반복
# 왼쪽 위에서 오는 경우
if i == 0: left_up = 0
else : left_up = dp[i - 1][j - 1]
- 만약 i가 0이라면 왼쪽이 없으므로 left_up이 없으니까 0
- i가 0 이 아니라면 왼쪽위에서 오는 경우를 left_up이라는 변수로 두고 이 경우 dp테이블의 d[i - 1][j -1]
- 첫번째 i,j는 위에서보면 i = 0, j = 1 그러나
| 왼쪽 위에서 오는 경우 | if i == 0: left_up = 0 else : left_up = dp[i - 1][j - 1] |
|
| i = 0, j = 1 좌표(0,1) | left_up = 0 | (0,1)의 왼쪽 위에서 오는 경우는 없음 |
| i = 0, j = 2 좌표(0,2) | left_up = 0 | (0,2)의 왼쪽 위에서 오는 경우는 없음 |
| i = 1, j = 1 좌표(1,1) | left_up = dp[0][0] 즉 (0,0) | (1,1)의 왼쪽 위에서 오는 경우는 (0,0) |
| i = 1, j = 2 좌표(1,2) | left_up = dp[0][1] 즉 (0,1) | (1,2)의 왼쪽 위에서 오는 경우는 (0,1) |
| i = 2, j = 1 좌표(2,1) | left_up = dp[1][0] 즉 (1,0) | (2,1)의 왼쪽 위에서 오는 경우는 (1,0) |
| i = 2, j = 2 좌표(2,2) | left_up = dp[1][1] 즉 (1,1) | (2,2)의 왼쪽 위에서 오는 경우는 (1,1) |
# 왼쪽 아래서 오는 경우
if i == n - 1: left_down = 0
else : left_down = dp[i + 1][j -1]
- n에 3을 입력받았다면 i == 2: left_down = 0
| 왼쪽 아래서 오는 경우 | if i == n - 1: left_down = 0 else : left_down = dp[i + 1][j -1] |
|
| i = 0, j = 1 좌표(0,1) | left_down = dp[1][0] 즉 (1,0) | (0,1)의 왼쪽 아래서 오는 경우는 (1,0) |
| i = 0, j = 2 좌표(0,2) | left_down = dp[1][1] 즉 (1,1) | (0,2)의 왼쪽 아래서 오는 경우는 (1,1) |
| i = 1, j = 1 좌표(1,1) | left_down = dp[2][0] 즉 (2,0) | (1,1)의 왼쪽 아래서 오는 경우는 (2,0) |
| i = 1, j = 2 좌표(1,2) | left_down = dp[2][1] 즉 (2,1) | (1,2)의 왼쪽 아래서 오는 경우는 (2,1) |
| i = 2, j = 1 좌표(2,1) | left_down = 0 | (2,1)의 왼쪽 아래서 오는 경우는 없음 |
| i = 2, j = 2 좌표(2,2) | left_down = 0 | (2,2)의 왼쪽 아래서 오는 경우는 없음 |
# 왼쪽에서 오는 경우
left = dp[i][j - 1]
dp[i][j] = dp[i][j] + max(left_up, left_down, left)
| 왼쪽에서 오는 경우 | left = dp[i][j - 1] dp[i][j] = dp[i][j] + max(left_up, left_down, left) |
|
| i = 0, j = 1 좌표(0,1) | left = dp[0][0] 즉 (0,0) dp[0][1] = dp[0][0] + max(left_up, left_down, left) |
(0,1)의 왼쪽에서 오는 경우는 (0,0) (0,1)에 ((0,0)의 값 + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
| i = 0, j = 2 좌표(0,2) | left = dp[0][1] 즉 (0,1) dp[0][2] = dp[0][1] + max(left_up, left_down, left) |
(0,2)의 왼쪽에서 오는 경우는 (0,1) (0,2)에 ((0,1)의 값 + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
| i = 1, j = 1 좌표(1,1) | left = dp[1][0] 즉 (1,0) dp[1][1] = dp[1][0] + max(left_up, left_down, left) |
(1,1)의 왼쪽에서 오는 경우는 (1,0) (1,1)에 ((1,0)의 값 + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
| i = 1, j = 2 좌표(1,2) | left = dp[1][1] 즉 (1,1) dp[1][2] = dp[1][1] + max(left_up, left_down, left) |
(1,2)의 왼쪽에서 오는 경우는 (1,1) (1,2)에 ((1,1)의 값 + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
| i = 2, j = 1 좌표(2,1) | left = dp[2][0] 즉(2,0) dp[2][1] = dp[2][0] + max(left_up, left_down, left) |
(2,1)의 왼쪽에서 오는 경우는 (2,0) (2,1)에 ((2,0)의 값 + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
| i = 2, j = 2 좌표(2,2) | left = dp[2][1] 즉 (2,1) dp[2][2] = dp[2][1] + max(left_up, left_down, left) |
(2,2)의 왼쪽에서 오는 경우는 (2,1) (2,2)에 ((2,1의 값) + (왼쪽위,왼쪽아래,왼쪽))의 최대값으로 갱신 |
result = 0
for i in range(n):
result = max(result, dp[i][m - 1])
- result 값은 0 을 시작으로
- n에 3을 입력 받았으면 0~2까지 하나씩 꺼낸 i를 아래 반복
- m도 3을 입력 받았으니까 아래중의 맥스값을 result에 저장
- 첫번째 result = max(0, (0,2))
- 두번째 result = max(0, (1,2))
- 세번째 result = max(0, (2,2))
- 단 지금의 반복문은 위의 값을 구한 후에 돌리는 반복문!
print(result)
- result값 출력
출처 / 유튜브 [동빈나 - (이코테2021) 이것이 취업을 위한 코딩 테스트다 with 파이썬]
'코딩테스트 연습' 카테고리의 다른 글
| 코테 연습) 최단경로 (0) | 2022.08.01 |
|---|---|
| 코테 연습) 다이나믹 프로그래밍 : 피보나치 수열(문제 : 병사 배치하기).python (0) | 2022.07.27 |
| 코테 연습) 다이나믹 프로그래밍 : 피보나치 수열(문제 : 효율적인 화폐 구성).python (0) | 2022.07.26 |
| 코테 연습) 다이나믹 프로그래밍 : 피보나치 수열(문제 : 1로 만들기).python (0) | 2022.07.26 |
| 코테 연습) 다이나믹 프로그래밍 : 피보나치 수열(문제 : 개미 전사).python (0) | 2022.07.25 |




